Странный аттрактор Лоренца
Модель служит для понимания хаотических систем, когда небольшие отклонения в начальных данных приводят к непредсказуемым последствиям.
Метеоролог Эдвард Нортон Лоренц обнаружил, что гидродинамические уравнения, которые он придумал для описания переносов воздуха в атмосфере, очень чувствительны к начальным данным. Таким образом появилась известная фраза, что взмах крыльев бабочки в Бразилии может вызвать торнадо в Техасе. Лоренц исследовал следующие уравнения, где x, y, z связаны со скоростью, плотностью и температурой потоков.
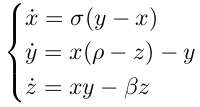
Аттрактором называют типичную картину в пространстве переменных системы уравнений, когда система стремится к равновесию по спирали или крутится вокруг точки фокуса. Система уравнений Лоренца продемонстрировала очень нетипичный аттрактор с хаотическим переключением между двумя точками фокуса, поэтому такой аттрактор назвали «странным аттрактором Лоренца». Данный пример стал классической демонстрацией того, что физические системы могут быть полностью детерминированными и в то же время непредсказуемыми по своей природе.
Изучите, как чувствительно решение к внесению возмущений в начальные данные. Параметр delta задает отклонения для начальных данных второй траектории, которая рисуется зелёным цветом. Переход из одного фокуса аттрактора в другой физически означает сильную смену погоды, а значит даже при наличии самой точной модели для расчётов небольшие погрешности оценки начальных данных приводят к невозможности точного предсказания погоды на длительный срок.
| Oberon & OberonJSSource code | Result |
|
|